Statistical Arbitrage Week1

Statistical Arbitrage applies equity long-short market neutral without human overlay and rebalanced around in 1 week to 1 month.

Typical Stat Arb

• Realized (not backtested) Sharpe Ratio > 2
• Make profit over any 6-months period
• Leverage: for \$1M capital, go \$2M long and \$2M short
• Scalable up to \$250M capacity
• Globally (developed equity markets only)
• Long-term sustainable through research

Requirement

• Managing complexity
• 10,000+ lines of code, 100’s of databases
• Must retain intellectual control at all times
• Need to “feel” the model and the markets
• Box is black to others, transparent to you

Toolkit

• Linear Algebra
• Statistics
• Economics
• Finance
• Optimization
• Programming

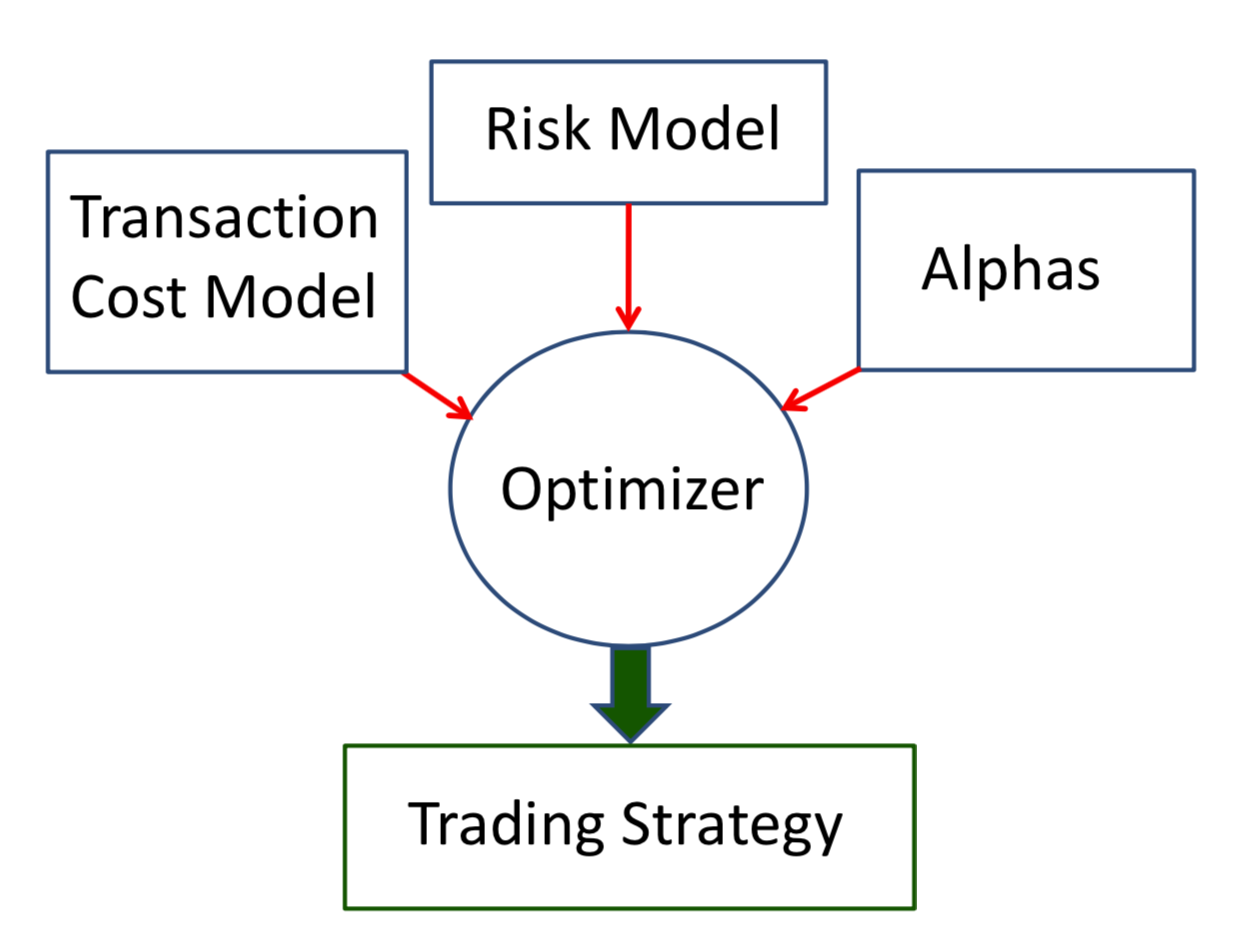
Main Component

• Alphas
• Risk Model (covariance matrix)
• T-cost model

• Optimizer

• Overall Structure of Main Components

Alphas

\(\alpha\) is a matrix of dimension \(T \times n\)

• \(T\) = number of days in the backtest
• \(n\) = number of stocks in your universe

$$\begin{bmatrix} \alpha_{1,1} & \alpha_{1,2} & \alpha_{1,3} & \dots & \alpha_{1,n} \\ \alpha_{2,1} & \alpha_{2,2} & \alpha_{2,3} & \dots & \alpha_{2,n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \alpha_{T,1} & \alpha_{T,2} & \alpha_{T,3} & \dots & \alpha_{T,n} \end{bmatrix}$$

Sample Steps to Process Alpha

Let \(m_{t,i}\) be the relative change at day \(t\).

1. Demean
   • \(x_{t,i} = m_{t,i} - (m_{t,1} + \ldots + m_{t,n})/n\)
2. Standardize
   • \(y_{t,i} = \frac{x_{t,i}}{\sqrt{\sum_{j=1}^{n}{x_{t,j}^2}/{(n-1)}}}\)
3. Windsorize
   • \(\alpha_{t,i} = y_{t,i} \;\text{if} \; \mid y_{t,i} \mid \leq 3\)
   • \(\alpha_{t,i} = 3 \; \text{if} \; y_{t,i} > 3\)
   • \(\alpha_{t,i} = -3 \; \text{if} \; y_{t,i} < -3\)

Risk Model

T-cost Model

Maximimum Trading Size

• 1% of Average Daily Volume (ADV)
• Capped so liquid stocks do not dominate

VWAP

• Volume-Weighted Average Price
• Typically: period = 1 day
• More advanced: period = 1 hour

Simple Transaction Cost Model

\(\text{commission} + 1\text{bp} + \text{median bid-ask spread}/2\)

Market Impact Model

\(I / \sigma = \text{constant} \cdot sign(X) \cdot \mid X/VT\mid ^\beta + \text{noise}\)

• \(I=\) temporary price impact
• \(\sigma=\) daily volatility
• \(X =\) trade size
• \(V =\) average daily volume
• \(T =\) trade duration (in days)

Permanent Price Impact

\(I / \sigma = \text{constant} \cdot (X/V) \cdot (\Theta/V) ^\delta + \text{noise}\)

• \(I=\) permanent price impact
• \(\Theta=\) shares outstanding
• \(X =\) trade size
• \(V =\) average daily volume

Optimizer

Notations

| Parameter | Dimension | Definition | |:-:|:-:|:-:| | \(x\) | \(n \times 1\) | vector of desired portfolio weights | | \(w\) | \(n \times 1\) | vector of initial portfolio weights | | \(\Sigma\) | \(n \times 1\) | covariance matrix of stock returns | | \(\alpha\) | \(n \times 1\) | vector of aggregate alphas | | \(\beta\) | \(n \times 1\) | vector of historical betas | | \(\tau\) | \(n \times 1\) | vector of transaction costs |

Objectives & Constraints

• Minimize risk: \(x’ \Sigma x\)
• Maximize exposure to alpha: \(\alpha’ x\)
• Neutralize exposure to beta: \(\beta’ x = 0\)
• Minimize transaction costs: \(\tau’ \lvert x-w \rvert\)

Objective Function

$max_{x} \underbrace{\alpha' x}_{\text{maximize alpha exposure}} - \overbrace{\lambda}^{\text{controls turnover}}\cdot \underbrace{\tau' \lvert x-w \rvert}_{\text{minimize transaction cost}} - \overbrace{\mu}^{\text{controls book size}}\cdot \underbrace{x' \Sigma x}_{\text{minimize portfolio variance}}$

$$\text{s.t}\; \beta' x = 0$$